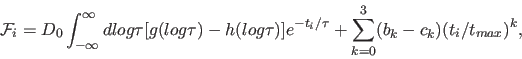 |
(1) |
The MEM
The MemExp program makes synergistic use of both the maximum entropy method (MEM) and maximum likelihood (ML) fitting to interpret kinetics data from the distributed and discrete perspectives. Its hybrid algorithm has been described in the literature [1]. MemExp version 2.0 extended the user's ability to manipulate the default model for kinetics involving overlapping phases [3]. Versions 3.0 and beyond support the rigorous ML analysis of Poisson data in addition to the treatment of Gaussian noise via nonlinear least-squares (NLS) fitting. Deconvolution of an instrument response function is supported for data that are equally spaced in time. A correction for scattered light was also first implemented in MemExp 3.0. New to version 4.0 was the easier-to-use 'auto' mode and a simple way to filter artifacts from the lifetime distribution HREF="node15.html#AB">2] by setting IBIGF = 3. Additional algorithmic details and applications of the MEM can be found elsewhere [4,5,6].
MemExp fits kinetics using one or two liftetime distributions:
When deconvolving an instrument response function R(t), corresponding to experimentally measured values ![]() , the data are described by:
, the data are described by:
The maximum entropy method (MEM) is used to obtain this fit ![]() by distributions. A MEM calculation is a
'tug of war' between two or three terms, depending on whether or not the normalization is to be constrained.
These terms are summed in the function Q,
by distributions. A MEM calculation is a
'tug of war' between two or three terms, depending on whether or not the normalization is to be constrained.
These terms are summed in the function Q,
The quality of the fit ![]() to the data
to the data ![]() produced by f is measured by C, which is a minimum (zero)
when the data and fit are everywhere equal. When analyzing data with normally distrbuted noise, C takes a familiar form:
produced by f is measured by C, which is a minimum (zero)
when the data and fit are everywhere equal. When analyzing data with normally distrbuted noise, C takes a familiar form:
| (7) |
| (8) |
The image normalization is given by
NLS and ML
Upon convergence of the MEM calculation, MemExp performs a series of fits to the
kinetics by ![]() discrete exponentials using either nonlinear least-squares (NLS) or maximum likelihood (ML) fitting:
discrete exponentials using either nonlinear least-squares (NLS) or maximum likelihood (ML) fitting:
When deconvolving a known instrument response function, R, these discrete fits take the form:
The value of C given by either equation 5 or 6 is calculated for both the continuous and the discrete fits,
facilitating a comparison of the distributed and discrete fits. The discrete fits are also characterized by either
Some Definitions
The graphical summaries output by MemExp (.out.ps and .exp.ps files) are labeled by several quantities,
including the values of C given by equations 5 (or 6) and 12. The correlation
length of the residuals ![]() is also reported for both the MEM and NLS/ML fits. It is estimated by summing the absolute value of
the autocorrelation function of the residuals over a span that depends on how slow the slowest process is.
The normalization of the fits are also given: I (equation 9) for the MEM fits and the sum of exponential
amplitudes,
is also reported for both the MEM and NLS/ML fits. It is estimated by summing the absolute value of
the autocorrelation function of the residuals over a span that depends on how slow the slowest process is.
The normalization of the fits are also given: I (equation 9) for the MEM fits and the sum of exponential
amplitudes, ![]() , for the discrete fits.
, for the discrete fits.
For the MEM fits, the value of Test [8] is also given (denoted as T). Test is zero when the
gradients of S and C are parallel. Test is therefore a good measure of convergence when only the Lagrange
multiplier ![]() is used (equation 3); small values of Test imply that the maximum-entropy solution
has indeed been found for the given value of C. Ratio is another measure of convergence that is
recorded in the .out files. Ratio is the norm of the gradient of Q divided by the norm of a unit vector [9].
Unlike Test, Ratio accounts for the effects of constraining the normalization I.
Ratio is therefore a good measure of convergence whether or not the Lagrange multiplier
is used (equation 3); small values of Test imply that the maximum-entropy solution
has indeed been found for the given value of C. Ratio is another measure of convergence that is
recorded in the .out files. Ratio is the norm of the gradient of Q divided by the norm of a unit vector [9].
Unlike Test, Ratio accounts for the effects of constraining the normalization I.
Ratio is therefore a good measure of convergence whether or not the Lagrange multiplier ![]() is used (equation 3).
If Test and Ratio both approach 1.0, the convergence should be slowed down by reducing EPSL and EPSU.
is used (equation 3).
If Test and Ratio both approach 1.0, the convergence should be slowed down by reducing EPSL and EPSU.