Normal Mode (Harmonic) Analysis

Normal modes of vibration are simple harmonic oscillations about a local energy minimum, characteristic of a system's structure $\vec{R}$ and its energy function $V(\vec{R})$. For a purely harmonic $V(\vec{R})$, any motion can be exactly expressed as a superposition of normal modes. For an anharmonic $V(\vec{R})$, the potential near the minimum will still be well approximated by a harmonic potential, and any small-amplitude motion can still be well described by a sum of normal modes. In other words, at sufficiently low temperatures, any classical system behaves harmonically.

In a typical normal mode analysis, the characteristic vibrations of an energy-minimized system ($T = 0^+$ K) and the corresponding frequencies are determined assuming $V(\vec{R})$ is harmonic in all degrees of freedom. Normal mode analysis is less expensive than MD simulation, but requires much more memory.

As a globular protein is heated from very low temperature, the fluctuations of its atoms begin to deviate measurably from harmonic behavior around 200 K. The motion at 300 K is considerably anharmonic. This must be kept in mind when attempting to interpret physiological behavior in terms of normal modes. Still, calculation of the normal mode spectrum is less expensive than a typical MD simulation, and the spectrum may provide qualitative, if not quantitative, insight.

The normal mode spectrum of a 3-dimensional system of N atoms contains $3N-6$ normal modes ($3N-5$ for linear molecules in 3D). In general, the number of modes is the system's total number of degrees of freedom minus the number of degrees of freedom that correspond to pure rigid body motion (rotation or translation). Each mode is defined by an eigenvector and its corresponding eigenfrequency, $\omega$. The eigenvector contains the amplitude and direction of motion for each atom. In mode i, all N atoms oscillate at the same frequency, $\omega_i$.

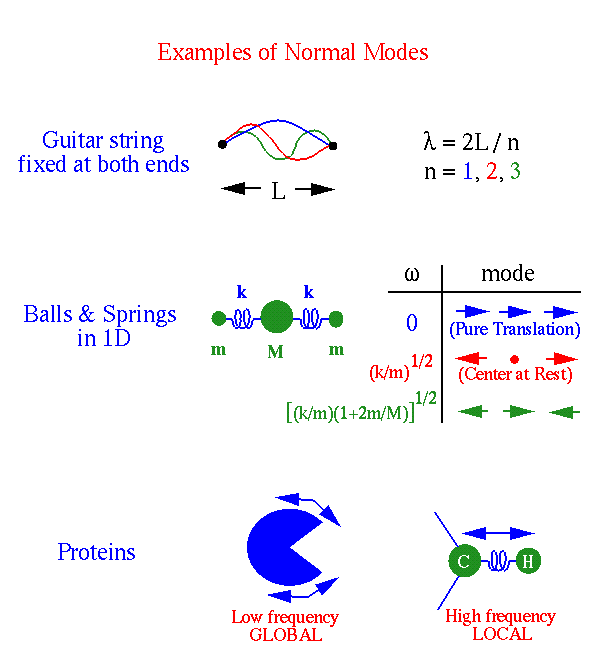Small oscillations about an equilibrium position
can be expressed in terms of normal modes.

In macromolecules, the lowest frequency modes correspond to delocalized motions, in which a large number of atoms oscillate with considerable amplitude. The highest frequency motions are more localized, with appreciable amplitudes for fewer atoms, e.g., the stretching of bonds between carbon and hydrogen atoms.